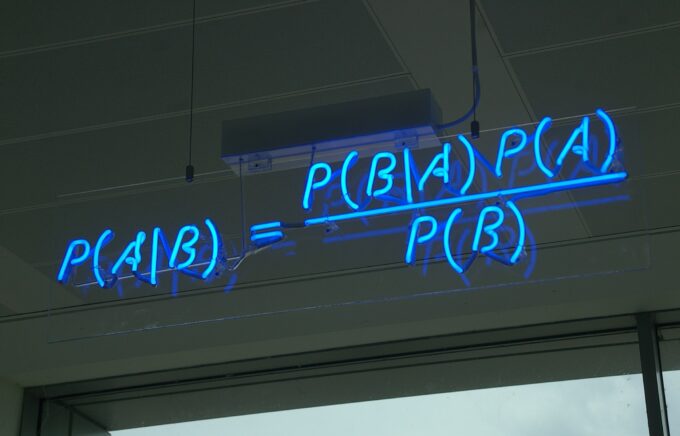Very often beginners are fooled by “professional” brokers, but they ask an interesting question: can a gambler have a hidden ability to predict or his bets are just the result of coincidence? This is almost a rhetorical question, because it is never possible to predict the outcome of any match with accuracy. The most common option is to calculate the probability of a random profit from a sample of bets. However the frequency approach under consideration is based only on a hypothesis that may indicate the presence of necessary skills for predicting or their absence, again only according to calculations.
The Bayes coefficient allows you to compare all the benefits of certain opinions without considering the true expectation. This method can be used to estimate the probability that a hypothesis is correct. The information observed over a certain period is taken as the basic data. If new information emerges, then it is perfectly acceptable to update the probability. Bayes’ theorem in betting has a significant drawback. If the unconditional probability (the certainty that a certain event has already happened, without previously analyzed and set conditions) is incorrectly chosen, it is possible to define a beginner as an established professional or vice versa.
However, the main task of the Bayes coefficient is to quantify the probability of one of the selected hypotheses, relative to the others, without considering the fact whether they are correct or not. This is indicated by the formula: BF = (P*(D|H1))/(P*(D|H0)). P is the probability, D is the data, and H is the hypothesis, respectively.
Application of Bayesian Theory in Betting by Example
Source: towardsdatascience.com
I want to consider two different examples, which should demonstrate the basic options for applying the theory in forecasting. In the first case, let’s take a soccer team that, according to bettors, fans and experts, wins away and plays best in rainy weather. It turns out that if the team plays away and it rains, you have to bet on a win and it will be a sure thing? Absolutely not and we will try to explain what can affect the result:
The weather factor. This is quite an important indicator, especially in the context of bettor observations. Also, few teams know how to play well on rainy days and prefer dry, sunny weather more.
Other indicators. These include: the level and class of teams, the presence/absence of leaders, motivation and other factors, such as refereeing errors, injuries during the match. If a team has to play with an outsider, but is scheduled to play in the finals of an important tournament in 3 days, it is unlikely there will be a 100% deduction.
Bayes’ theorem in action. The sample of games played in rainy weather is 50 games, 45 wins, that is 75% probability. In other conditions, the team has played 100 games and has 50 wins, i.e. 50% probability and it can already be calculated that in the first case the opportunities for earning are better. But common sense suggests that these are just numbers, calculated purely for statistics, essentially decisive.
An objective assessment of Bayesian theory demonstrates a significant dependence on the number of matches played and various factors that are not included in the formula.
Let’s try to look at the peculiarities of calculations, from the other side. For example, bets are made on sports, where there are only 2 main outcomes: the victory of one team/athlete or the other. Suppose the first club plays better at home, because they win 7 of 10 matches. Let’s hypothesize that the odds of winning are 70% to 30%. If the statistics were the same: 5 wins and 5 losses – the odds are 50% to 50%, respectively. The third option for an in-depth study yielded results of 60% to 40%. Which hypothesis can be considered correct?
If we use the frequency approach, the probability of 60% of wins when the hypothesis is 50/50 is only up to 2%, which is extremely low to confirm the bias of the results. Although it does denote the fairness of the process. According to Bayesian theory, you can compare the probability of each hypothesis without considering all their advantages with respect to a particular event.
Important Nuances of the Bayesian Theorem
Source: modinst.lu.lv
If you take into account all the features of the theorem in question, it is not immediately clear what exactly needs to be calculated. In fact, the Bayes coefficient is quite a complex solution, which requires a lot of attention when considering it in its entirety. It is worth highlighting the following nuances, which allow at least on a basic level to understand the meaning of the theorem:
The results of the data being analyzed cannot be considered events. In simple words, there is a strategy for calculating the passage of a particular bet and the match itself, which is used for analysis. If a bettor decides to make a bet, it is not a fact that he will confirm it and make a deposit. That is, all probabilities need to be considered separately, as specific hypotheses. Only in this way it is possible to calculate at least approximately a certain chance of winning. If you mix research results, analytics and events, applying Bayesian theorem, the results will be very unclear and there is no efficiency to speak of.
The effect of errors on the result. When the bettor analyzes the match, he can determine the information that does not correspond to reality (false positive), as well as miss the facts presented in fact (false negative). As a result, even a qualitatively composed analysis will be inherently wrong, and Bayes’ formula will not help in any way.
The theorem is not considered ideal for calculations. Many will wonder why we write about it at all then, if efficiency does not exist? It does exist, but it is important to constantly consider the mass of options that fall into the category of error.
It is also worth noting that even in science, any fact is considered only a certain result for the application of a particular strategy. Well, or is its indicator. If we take philosophy into account, any experiment would only be a study of a particular process with a probability of error. For obvious reasons, Bayes’ theorem or Kelly’s criterion is nowhere near 100% accurate. But no one is saying that a proven strategy has to give a perfect score. In that case, the betting companies would not exist at all, because of the superiority of the players.
Source: unsplash.com
The point of Bayes’ theorem for betting is not at all to find the probability that team A is 75% better than team B. It is meant to find out the true state of affairs, by testing different hypotheses. If studying the line, researching all the facts around a certain event is perfect and accurate, then the two probabilities should match. In the end, all positive outcomes will be the same as negative ones. In fact, Bayes’ formula will allow.
Source: BookmakerAdvisor